Last week, I used the Graph Model of Conflict Resolution to find a set of stable equilibria in the present conflict between North Korea and the USA. They were:
- The tense status quo (s. 0)
- An American troop withdrawal, paired with North Korea giving up its nuclear weapons (s.10)
- All out conventional warfare on the Korean Peninsula (s. 4)
- All out nuclear warfare on the Korean Peninsula (s. 5)
But how much can we trust these results? How much to they depend on my subjective ranking of the belligerent’s preferences? How much do they depend on the stability metrics I used?
To get a sense of this, I’m going to add another stability metric into the mix, come up with three new preference vectors, and look at how the original results change when we consider a North Korean invasion to be irreversible. After these eight new stability calculations, we’ll have nine slightly different ways of looking at the conflict; this should help us guess which equilibria are robust to my subjective choices and which might exist only because of how I framed the problem.
Alternative Stability Metrics
Previously we assessed stable states using Nash Stability and Sequential Stability. Sequential Stability allowed us to see what would happen if the decision makers were looking two moves ahead and assuming that their opponents wouldn’t “cut off the nose to spite the face” – it assumes, in essence, that people will only sanction by moving to states that they like more, not states they like less.
Maybe that’s a bad assumption dealing with Trump and Kim Jong-un. In this case, wouldn’t it be better to use Symmetric Metarationality? With Symmetric Metarationality, all sanctioning unilateral moves are on the table. Symmetric Metarationality also allows decision makers to respond to sanctioning. In effect, it lets them look three moves ahead, instead of the two allowed by Sequential Stability.
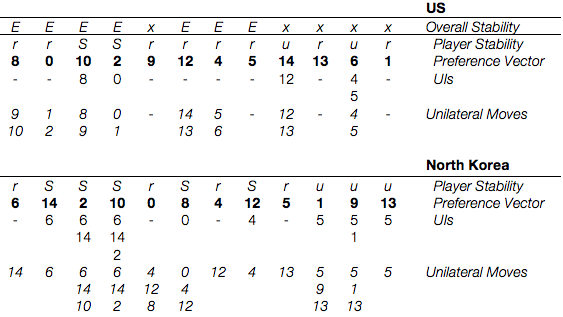
Before we see how this new metric changes things, let’s review our states, preference vectors, and stability analysis from last time.
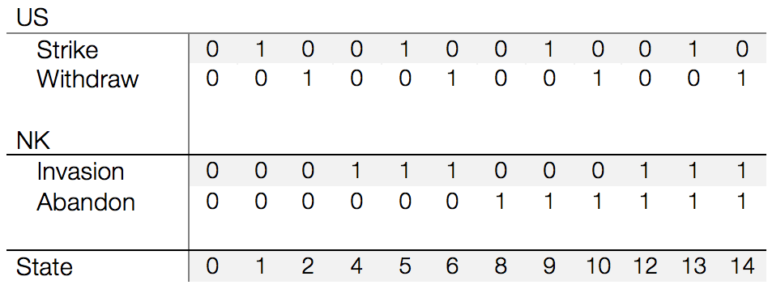
The states are:
Or in plain English:
| State | Explantation |
|---|---|
| 0 | Status quo |
| 1 | Nuclear strike by the US, NK keeps nuclear weapons |
| 2 | Unilateral US troop withdrawal |
| 4 | North Korean invasion with only conventional US responses |
| 5 | North Korean invasion with US nuclear strike |
| 6 | US withdrawal and North Korean Invasion |
| 8 | Unilateral North Korean abandonment of nuclear weapons |
| 9 | US strike and North Korean abandonment of nuclear weapons |
| 10 | Coordinated US withdrawal and NK abandonment of nuclear weapons |
| 12 | NK invasion after abandoning nuclear weapons; conventional US response |
| 13 | NK invasion after abandoning nuclear weapons; US nuclear strike |
| 14 | US withdrawal paired with NK nuclear weapons abandonment and invasion |
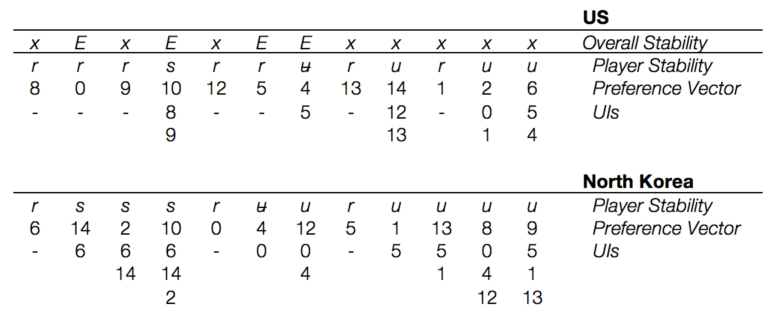
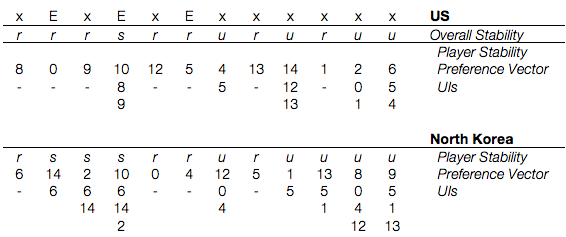
From these states, we saw the following equilibria and unilateral improvements:
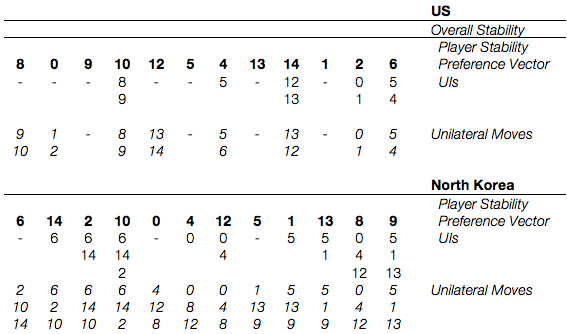
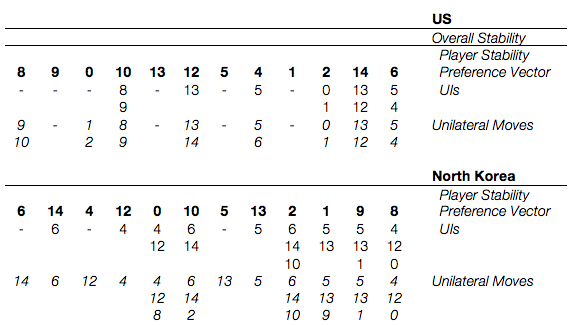
When dealing with Symmetric Metarationality, I find it very helpful to modify the chart above so that it also includes unilateral moves. After we make this change and blank out our results, we get the following:
From here, we use a simple algorithm. First, all states without unilateral improvements are Nash Stable. Next, we check each unilateral improvement in the remaining states against the opponent’s unilateral actions, then against the original actors best unilateral action from each of the resulting states. If there are no results lower than the original actor started, the move is unstable. Otherwise it’s stable by Symmetric Metarationality (and we’ll mark it with “S”). Like Sequential Stability, you can’t truly call this done until you check for states that are simultaneously sanctioned (this is often easy because simultaneous sanctioning is only a risk when both sides are unstable).
An example: There exist a unilateral improvement for America from s. 4 to s. 5. From s. 5, North Korea can move to s. 1, 13, or 9. America disprefers both s. 1 and s. 13 to s. 4 and has no moves out of them, so the threat of North Korea taking either of those actions is an effective sanction and makes s. 4 stable on the American side.
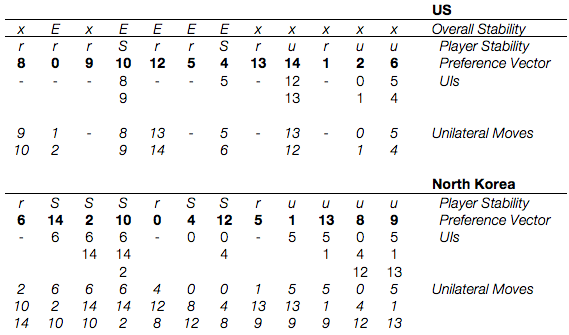
Once we repeat this for all states across both sides, we get the following:
We’ve kept all of our old equilibria and gained a new one in s. 12: “NK invasion after abandoning nuclear weapons; conventional US response”.
Previously, s. 12 wasn’t stable because North Korea preferred the status quo (s. 0) to it and the US had no UIs from the status quo. North Korea moving from s. 12 to s. 0 is sanctioned in Symmetric Metarationality by the US unilateral move from s. 0 to s. 1, which leaves North Korea with only the option of moving from s. 1 to s. 5. State 5 is dispreferred to s. 12 by North Korea, so it can’t risk leaving s. 12 for s. 0. State 12 was always Nash Stable for the US, so it becoming stable for North Korea makes it an equilibrium point.
To put this another way (and to put an example on what I said above), using Symmetric Metarationality allows us to model a world where the adversaries see each other as less rational and more spiteful. In this world. NK doesn’t trust the US to remain at s. 0 if it were to call for a truce after an invasion, so any invasion that starts doesn’t really end.
It was heartening to see all of our existing equilibria remain where they were. Note that I did all of the work in this post without knowing what the results would be and fully prepared to publish even if my initial equilibria never turned up again; that they showed up here made me somewhat relieved.
Irreversible Invasions
Previously we modelled invasions as reversible. But is this a realistic assumption? It’s very possible that the bad will from an invasion could last for quite a while, making other strategies very difficult to try out. It’s also likely that America wouldn’t just let North Korean troops give up and slink away without reprisal. If this is the case, maybe we should model a North Korean invasion as irreversible. This will mean that there can be no unilateral improvements for North Korea from s. 4, 5, or 6 to s. 0, 1, 2, 8, 9, or 10.
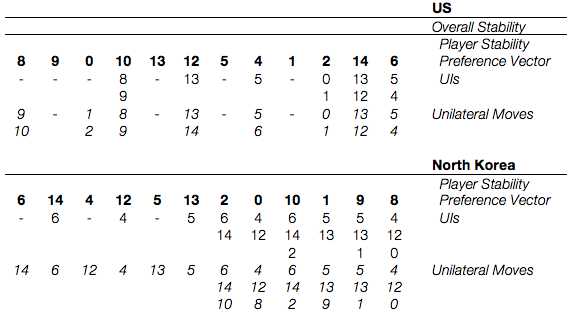
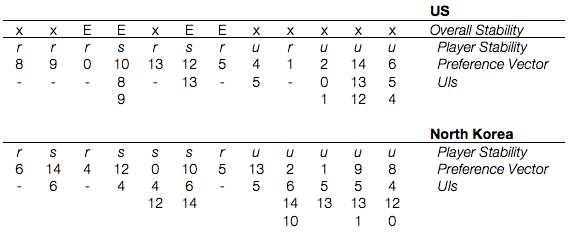
In practical terms, modelling an invasion as irreversible costs North Korea one unilateral improvement, from s. 4 to s. 0. Let’s see if this changes the results at all (we’re back to sequential stability):
We end up losing the simultaneous sanctioning that made s. 4 a stable state, leaving us with only three stable states: the status quo, a trade of American withdrawal for the North Korean nuclear program, and all out nuclear war on the Korean Peninsula.
We’ve now tried three different ways of looking at this problem. Three equilibria (s. 0, 10, 5) showed up in all cases, one in two cases (s. 4), and one in one case (s. 12). We’re starting to get a sense for which equilibria are particularly stable and which are more liable to only pop up under certain conditions. But how will our equilibria fare when faced with a different preference vectors?
Bloodthirsty Belligerents
What if we’ve underestimated how much North Korea and the United States care about getting what they want and overestimated how much they care about looking reasonable? I’m going to try ranking the states so that North Korea always prefers invading and the US always prefers first that North Korea doesn’t invade the South and second that they have no nuclear weapons program.
This gives us the following preference vectors:
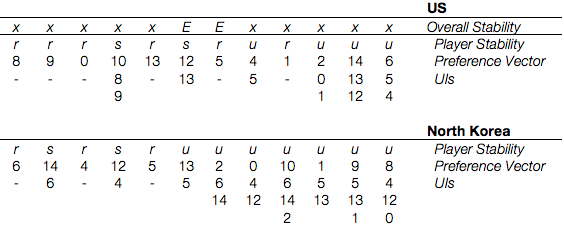
- US: 8, 9, 0, 10, 13, 12, 5, 4, 1, 2, 14, 6
- NK: 6, 14, 4, 12, 5, 13, 2, 0, 10, 1, 9, 8
Since we’re modelling the actors as more belligerent, let’s also assume for the purposes of these analyses that invasions are irreversible.
Here are the preferences vectors we’ll use to find equilibria:
Sequential Stability
Here we have only two stable states, s. 5 and 12. Both of these involve war on the Korean Peninsula; not even the status quo is stable. State 2 is at risk of simultaneous sanctioning, but the resulting states (4, 12, 5, 13) aren’t dispreferred, to s. 2 for either actor, so no simultaneous sanctioning occurs. There really are just two equilibria.
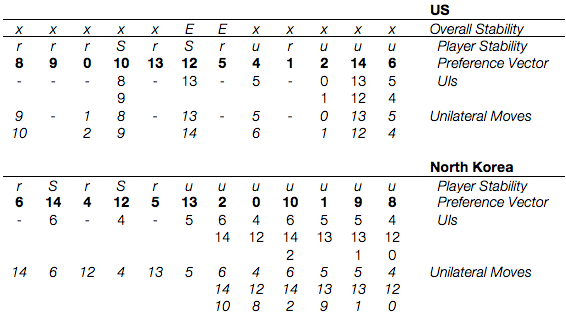
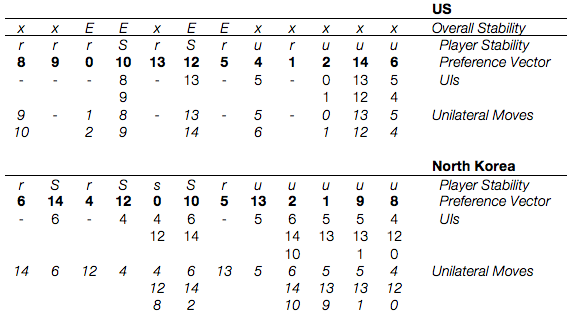
Symmetric Metarationality
Symmetric Metarationality gives us the exact same result. Only s. 5 and s. 12 are stable. This is suspicious, as the conflict has managed to stay in s. 0 for quite some time. If these preferences were correct, North Korea would have already invaded South Korea and been met with a nuclear response.
What if these preferences are substantially correct and both sides are more aggressive than we initially suspected, but North Korea disprefers being attacked by nuclear weapons below s. 0 and s. 10? That state of affairs is perhaps more reasonable than the blatantly suicidal North Korea we just imagined. How does a modicum of self-preservation change the results?
Nuclear Deterrence
If we’re assuming that North Korea has broadly similar preferences to our last variation, but doesn’t want to get attacked by nuclear weapons, we get the following preference vectors:
- US: 8, 9, 0, 10, 13, 12, 5, 4, 1, 2, 14, 6
- NK: 6, 14, 4, 12, 0, 10, 5, 13, 2, 1, 9, 8
Here are the annotated preferences vectors we’ll use to assess stability with Sequential Stability and Symmetric Metarationality. Since we’re leaving the belligerency of the United States the same, we’ll continue to view invading as an irreversible action.
Sequential Stability
One “minor” change – deciding that North Korea really doesn’t want to be nuked – and we again have the status quo and a negotiated settlement (in addition to two types of war) as stable equilibria. Does this hold when we’re using Symmetric Metarationality?
Symmetric Metarationality
Again, we have s. 0, 5, 10, and 12 as our equilibria.
As we’ve seen throughout, Symmetric Metarationality tends to give very similar answers to Sequential Stability. It’s still worth doing – it helps reassure us that our results are robust, but I hope by now you’re beginning to see why I could feel comfortable making an initial analysis based just off of just Sequential Stability.
Pacifistic People
What instead of underestimating the bloodthirstiness of our belligerents, we’ve been overestimating it? It’s entirely possible that both sides strongly disprefer all options that involve violence (and the more violence an option involves, the more they disprefer it) but talk up their position in hopes of receiving concessions. In this case, let’s give our actors these preference vectors:
- US: 8, 0, 10, 2, 9, 12, 4, 5, 14, 13, 6, 1
- NK: 6, 14, 2, 10, 0, 8, 4, 12, 5, 1, 9, 13
(Note that I’m only extending “peacefulness” to these two actors; I’m assuming that North Korea would happily try and annex South Korea if there was no need to fight America to do so)
There are fewer unilateral improvements in this array than in many of the previous ones.
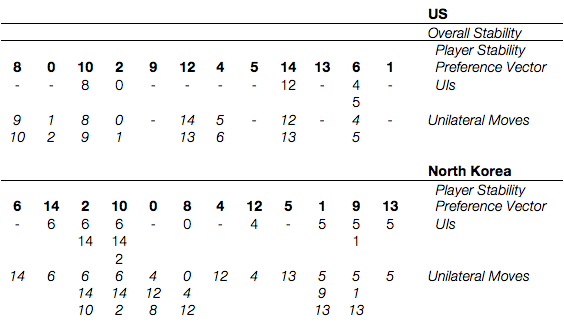
Sequential Stability
This is perhaps the most surprising result we’ve seen so far. If both powers are all talk with nothing behind it and both powers know and understand this, then they’ll stick in the current high-tension equilibria or fight a war. The only stable states here are s. 0, 4, and 5. State 10, the “negotiated settlement” state is entirely absent. We’ll revisit this scenario with hypergame analysis later, to see what happens if the bluff is believed.
Symmetric Metarationality
Here we see more equilibria than we’ve seen in any of the other examples. States 2 (unilateral US withdrawal) and 8 (North Korea unilaterally abandoning its nuclear weapons program) make their debut and s. 0, 4, 5, 10, and 12 appear again.
Remember, Symmetric Metarationality is very risk averse; it considers not just opponents’ unilateral improvements, but all of their unilateral moves as fair game. The fact that s. 0 has unilateral moves for either side that are aggressive leaves the actors too scared to move to it, even from states that they disprefer. This explains the presence of s. 2 and s. 8 in the equilibrium for the first time; they’re here because in this model both sides are so scared of war that if they blink first, they’ll be more relieved at the end of tension than they will be annoyed at moving away from their preferences.
I think in general this is a poor assumption, which is why I tend to find Sequential Stability a more useful concept than Symmetric Metarationality. That said, I don’t think this is impossible as a state of affairs, so I’m glad that I observed it. In general, this is actually one of my favourite things about the Graph Model of Conflict Resolution: using it you can very quickly answer “what ifs”, often in ways that are easily bent to understandable narratives.
Why Sensitivity Analysis?
The cool thing about sensitivity analysis is that it shows you the equilibria a conflict can fall into and how sensitivity those equilibria are to your judgement calls. There are 12 possible states in this conflict, but only 7 of them showed up in any stability analysis at all. Within those seven, only 5 showed up more than once.
Here’s a full accounting of the states that showed up (counting our first model, there were nine possible simulations for each equilibrium to show up in):
| State | Explantation | # |
|---|---|---|
| 0 | Status quo | 7 |
| 2 | Unilateral US troop withdrawal | 1 |
| 4 | North Korean invasion with only conventional US responses | 4 |
| 5 | North Korean invasion with US nuclear strike | 9 |
| 8 | Unilateral North Korean abandonment of nuclear weapons | 1 |
| 10 | Coordinated US withdrawal and NK abandonment of nuclear weapons | 6 |
| 12 | NK invasion after abandoning nuclear weapons; conventional US response | 6 |
Of the five that showed up more than once, four showed up more than half the time. These then are the most robust equilibria; equilibria that half of the reasonable changes we attempted couldn’t dislodge.
Note “most robust” is not necessarily equivalent to “most likely”. To get actual probabilities on outcomes, we’d have to put probabilities on the initial conditions. Even then, the Graph Model of Conflict Resolution as we’ve currently talked about it does little to explain how decision makers move between equilibria; because this scenario starts in equilibrium, it’s hard to see how it makes it to any of the other equilibria.
Hopefully I’ll be able to explain one way we can model changes in states in my next post, which will cover Hypergame Analysis – the tool we use when actors lack a perfect understanding of one another’s preferences.