It can be hard to grasp that radio waves, deadly radiation, and the light we can see are all the same thing. How can electromagnetic (EM) radiation – photons – sometimes penetrate walls and sometimes not? How can some forms of EM radiation be perfectly safe and others damage our DNA? How can radio waves travel so much further than gamma rays in air, but no further through concrete?
It all comes down to wavelength. But before we get into that, we should at least take a glance at what EM radiation really is.
Electromagnetic radiation takes the form of two orthogonal waves. In one direction, you have an oscillating magnetic field. In the other, an oscillating electric field. Both of these fields are orthogonal to the direction of travel.
These oscillations take a certain amount of time to complete, a time which is calculated by observing the peak value of one of the fields and then measuring how long it takes for the field to return to that value. Luckily, we only need to do this once, because the time an oscillation takes (called the period) will stay the same unless acted on by something external. You can invert the period to get the frequency – the number of times oscillations occur in a second. Frequency uses the unit Hertz, which are just inverted seconds. If something has the frequency 60Hz, it happens 60 times per seconds.
EM radiation has another nifty property: it always travels at the same speed, a speed commonly called “the speed of light”[^1] (even when applied to EM radiation that isn’t light). When you know the speed of an oscillating wave and the amount of time it takes for the wave to oscillate, you can calculate the wavelength. Scientists like to do this because the wavelength gives us a lot of information about how radiation will interact with world. It is common practice to represent wavelength with the Greek letter Lambda (λ).
Put in a more mathy way: if you have an event that occurs with frequency f to something travelling at velocity v, the event will have a spatial periodicity λ (our trusty wavelength) equal to v / f. For example, if you have a sound that oscillates 34Hz (this frequency is equivalent to the lowest C♯ on a standard piano) travelling at 340m/s (the speed of sound in air), it will have a wavelength of (340 m/s)/(34 s-1) = 10m. I’m using sound here so we can use reasonably sized numbers, but the results are equally applicable to light or other forms of EM radiation.
Wavelength and frequency are inversely related to each other. The higher the frequency of something, the smaller its wavelength. The longer the wavelength, the lower the frequency. I’m used to people describing EM radiation in terms of frequency when they’re talking about energy (the quicker something is vibrating, the more energy it has) and wavelength when talking about what it will interact with (the subject of the rest of this post).
With all that background out of the way, we can actually “look” at electromagnetic radiation and understand what we’re seeing.
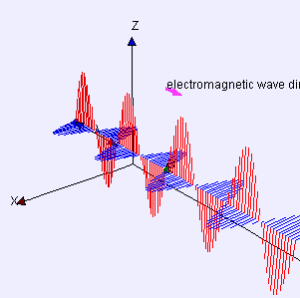
Wavelength is very important. You know those big TV antennas houses used to have?
Turns out that they’re about the same size as the wavelength of television signals. The antenna on a car? About the same size as the radio waves it picks up. Those big radio telescopes in the desert? Same size as the extrasolar radio waves they hope to pick up.
Even things we don’t normally think of as antennas can act like them. The rod and cone cells in your eyes act as antennas for the light of this very blog post[^2]. Chains of protein or water molecules act as antennas for microwave radiation, often with delicious results. The bases in your DNA act as antennas for UV light, often with disastrous results.
These are just a few examples, not an exhaustive list. For something to be able to interact with EM radiation, you just need an appropriately sized system of electrons (or electrical system; the two terms imply each other). You get this system of electrons more or less for free with metal. In a metal, all of the electrons are delocalized, making the whole length of a metal object one big electrical system. This is why the antennas in our phones or on our houses are made of metal. It isn’t just metal that can have this property though. Organic substances can have appropriately sized systems of delocalized electrons via double bonding[^3].
EM radiation can’t really interact with things that aren’t the same size as its wavelength. Interaction with EM radiation takes the form of the electric or magnetic field of a photon altering the electric or magnetic field of the substance being interacted with. This happens much more readily when the fields are approximately similar sizes. When fields are the same size, you get an opportunity for resonance, which dramatically decreases the loss in the interaction. Losses for dissimilar sized electric fields are so high that you can assume (as a first approximation) that they don’t really interact.
In practical terms, this means that a long metal rod might heat up if exposed to a lot of radio waves (wavelengths for radio waves vary from 1mm to 100km; many are a few metres long due to the ease of making antennas in that size) because it has a single electrical system that is the right size to absorb energy from the radio waves. A similarly sized person will not heat up, because there is no single part of them that is a unified electrical system the same size as the radio waves.
Microwaves (wavelengths appropriately micron-sized) might heat up your food, but they won’t damage your DNA (nanometres in width). They’re much larger than individual DNA molecules. Microwaves are no more capable of interacting with your DNA than a giant would be of picking up a single grain of rice. Microwaves can hurt cells or tissues, but they’re incapable of hurting your DNA and leaving the rest of the cell intact. They’re just too big. Because of this, there is no cancer risk from microwave exposure (whatever paranoid hippies might say).
Gamma rays do present a cancer risk. They have a wavelength (about 10 picometres) that is similar in size to electrons. This means that they can be absorbed by the electrons in your DNA, which kick these electrons out of their homes, leading to chemical reactions that change your DNA and can ultimately lead to cancer.
Wavelength explains how gamma rays can penetrate concrete (they’re actually so small that they miss most of the mass of concrete and only occasionally hit electrons and stop) and how radio waves penetrate concrete (they’re so large that you need a large amount of concrete before they’re able to interact with it and be stopped[^4]). Gamma rays are stopped by the air because air contains electrons (albeit sparsely) that they can hit and be stopped by. Radio waves are much too large for this to be a possibility.
When you’re worried about a certain type of EM radiation causing cancer, all you have to do is look at its wavelength. Any wavelength smaller than that of ultraviolet light (about 400nm) is small enough to interact with DNA in a meaningful way. Anything large is unable to really interact with DNA and is therefore safe.
Epistemic Status: Model. Looking at everything as antenna will help you understand why EM radiation interacts with the physical world the way it does, but there is a lot of hidden complexity here. For example, eyes are far from directly analogous to antennas in their mechanism of action, even if they are sized appropriately to be antennas for light. It's also true that at the extreme ends of photon energy, interactions are based more on energy than on size. I've omitted this in order to write something that isn't entirely caveats, but be aware that it occurs.</p>
[^1]: You may have heard that the speed of light changes in different substances. Tables will tell you that the speed of light in water is only about ¾ of the speed of light in air or vacuum and that the speed of light in glass is even slower still. This isn't technically true. The speed of light is (as far as we know) cosmically invariant – light travels the same speed everywhere in the galaxy. That said, the amount of time light takes to travel between two points can vary based on how many collisions and redirections it is likely to get into between two points. It's the difference between how long it takes for a pinball to make its way across a pinball table when it hits nothing and how long it takes when it hits every single bumper and obstacle.
[^2]: This is a first approximation of what is going on. Eyes can be modelled as antennas for the right wavelength of EM radiation, but this ignores a whole lot of chemistry and biophysics.
[^3]: The smaller the wavelength, the easier it is to find an appropriately sized system of electrons. When your wavelength is the size of a double bond (0.133nm), you'll be able to interact with anything that has a double bond. Even smaller wavelengths have even more options for interactions – a wavelength that is well sized for an electron will interact with anything that has an electron (approximately everything).
[^4]: This interaction is actually governed by quantum mechanical tunneling. Whenever a form of EM radiation "tries" to cross a barrier larger than its wavelength, it will be attenuated by the barrier. The equation that describes the probability distribution of a particle (the photons that make up EM radiation are both waves and particles, so we can use particle equations for them) is approximately 
(I say approximately because I've simplified all the constants into a single term, k), which becomes 
(here I'm using k1 to imply that the constant will be different), the equation for exponential decay, when the energy (to a first approximation, length) of the substance is higher than the energy (read size of wavelength) of the light.
This equation shows that there can be some probability – occasionally even a high probability – of the particle existing on the other side of a barrier. All you need for a particle to traverse a barrier is an appropriately small barrier.