Russell's Paradox

In a village, the barber shaves everyone who does not shave himself, but no one else. Who shaves the barber.
Imagine The Barber as similar to The Pope. When he is in his shop, cutting hair, he is The Barber and has all of the powers that entails, just as The Pope only possesses the full power of papacy when speaking “from the chair”. When The Barber isn’t manifesting this mantle, he’s just Glen, the nice fellow down the lane. Glen shaves his own beard. The Barber therefore doesn’t have to.
Alternatively, the barber is a woman.
Omnipotence Paradox

Can God create a rock so large that he himself cannot lift it?
It depends.
In Christian theology, God is often considered all-knowing, all-powerful, and all-loving. Some theologians dispute each of these, but most agree he has at least some mix of those three attributes. It turns out the answer to this paradox depends on which theologians are right.
This question is only interesting if god is all-powerful. If God isn’t all powerful, then this question will be determined by which is greater: his power of creation, or his power to manipulate creation. That’s a boring answer, so let’s focus on the cases where God is all powerful.
If God is all-knowing, then we’ll probably be left unsatisfied. God will know if he can or cannot create the boulder, so he’ll probably feel no need to test if he can.
If God is not all-knowing but is all-loving, then the question will only be answered if God cannot lift the first boulder he creates. If he can lift the first one, he will quickly realize that he could end up spending all of eternity trying to make a big enough boulder on the off chance that this is the one he finally cannot lift. An all-loving God would not abandon his flock for such a meaningless task, so we’ll never see the answer.
If God is neither all-knowing nor all-loving and has at least a bit of curiosity, then we should be able to eventually observe him trying to create a boulder large enough that he cannot lift it. This God won’t know the answer and wouldn’t necessarily care that finding out requires abandoning all of his other duties.
Given that this question was first posed right before the crusades, I believe that we’re experiencing the third scenario. The mere act of raising this paradox caused God to turn his face away from the world and worry about more interesting problems than those caused by a bunch of jumped up apes.
Zeno's Paradox
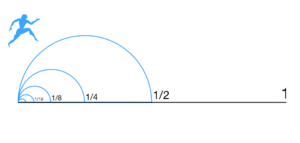
If you want to go somewhere, you first have to get halfway there. But to get to the midpoint, you have to go a quarter of the way. But to get to a quarter… When you subdivide like this, you’ll see that there are an infinite number of steps you must take to go anywhere. You cannot accomplish an infinite number of tasks in a finite time, therefore, movement is impossible.
It’s a common mistake that space is infinitely sub-dividable. In fact, there is a limit to how finely you can cut space. You cannot cut the universe more finely than 1.61x 10-35m, a length called the Planck Length. The Planck length is to the width of a hair as the width of a hair is to the whole universe. It’s an unimaginably tiny length.
An important property of halving things: you get really small numbers very quickly. If you halve a distance of 1m a mere 116 times, you’ll have cut the distance as finely as it is possible to cut anything. At this point, you can halve the distance no more and you can proceed to your destination, one Planck length at a time.
Sorites Paradox

There is a pile of sand in front of you. If you remove a grain of sand from it, it will still be a pile. If you remove another, it will still be a pile. But if you keep removing them, eventually it won’t be. When does it stop being a pile?
I’m emailing ISO and the NIST about this one. I expect to have an answer after ten years and three hundred committee meetings.
The Ship of Theseus

The Athenian Theseus bequeathed his ship to the city. As the ship aged, the Athenians kept it in perfect condition by replacing any planks and fittings that rotted away. Eventually, the entire ship had been replaced. This caused all of the philosophers in Athens to wonder: was it still Theseus’s Ship.
We could leave this one to ISO as well, but luckily as a Canadian I have another recourse.
The Comprehensive Economic and Trade Agreement between the EU (of which Greece is a member) and Canada considers a car “Made in Canada” or “Made in Europe” if at least 50% of the car came from there and at least 20% of the manufacturing occurred there.
Treating boats with a similar logic, we can see that as long as the Athenians were using local materials and labour (and weren’t outsourcing to the Persians or Phoenicians), the ship would count as “Made in Greece”. Since the paradox specifically states that the Athenians were doing all the restoring, this is probably a safe assumption.
If we take this and assume that Theseus had a solid grounding in trademark law – which would allow us to assume that he made his ship a protected brand like Harris Tweed, Kobe beef, Navaho, and Scotch – then we can see that the ship would still fall under the Theseus’s Ship™ brand. Most protected brands require a certain geographic origin, but we’ve already been over that in this case.
Even when philosophers argue that the boat is no longer Theseus’s Ship, they have to admit it is Theseus’s Ship™.
Unexpected Hanging Paradox

A prisoner is sentenced to hanging by a judge. The judge stipulates that the sentence will be carried out on one of the days in the next week, that it will be carried out before noon, and that it must be a surprise to the prisoner.
The prisoner smirks, believing he will never be hung. He knows that if it is Thursday at noon and he hasn’t been hung, then the hanging would have to be on Friday. But then it wouldn’t be a surprise. So logically, he has to be hung before Friday. If this is the case though, he can’t be hung on Thursday, because if he hasn’t been hung by noon on Wednesday then a hanging on Thursday won’t be a surprise. Following through this logic, the prisoner could only be hung on the Monday. But then it will be no surprise at all!
This is indeed a problem if the judge is as good at logic as the prisoner. But if the judge remains blissfully unaware of logical induction, there is no paradox here. The judge will assume that by picking a day at random she can surprise the prisoner. The prisoner will no doubt be quite surprised when he is hung.
This becomes more likely if we set the problem in America, where some judges are elected and therefore aren’t governed by anything so limiting as qualifications.
